Téma: Měření délky posuvným měřidlem
 Úkol: Změřte vnitřní průměr, vnější průměr a hloubku kádinky.

     Teoretická příprava: Posuvné měřidlo slouží k přesnému měření vnějších a vnitřních rozměrů strojních součástí.

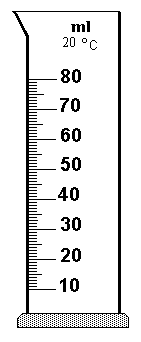
 Téma: Objem kapaliny
 Úkol: Změřte objem kapaliny v odměrném válci.

     Teoretická příprava: Objem tělesa je fyzikální veličina, značí se V a udává, jakou část prostoru dané těleso zaujímá.

Jednotky objemu:

1m³…………metr krychlový

1dm³ = 0,001 m³

1cm³ = 0,000 001 m³

1mm³ = 0,000 000 001 m³

1hl ..... hektolitr (1hl = 100l 1hl = 0,1m³)

1l ..... litr (1 l = 10dl 1 l = 1dm³)

1dl ..... decilitr (1 l = 100cl 1ml = 1cm³)

1cl ..... centilitr

1 ml ..... mililitr

Nádoby pro měření objemu:

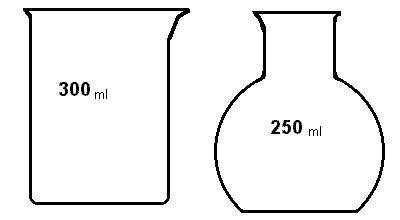odměrný válec	nádoby pro odměření určitého objemu

 Téma: Objem pevného tělesa.
 Úkol: Změřte objem pevného tělesa pomocí odměrného válce.

     Teoretická příprava: Při ponoření pevného tělesa do kapaliny se hladina kapaliny zvýší. Objem tělesa V vypočteme: V = V₂ - V₁
V₁ - je objem kapaliny
V₂ - je objem kapaliny s tělesem

 Téma: Pružina
 Úkol: Určete závislost délky pružiny na počtu závaží.

     Teoretická příprava: Země působí na závaží gravitační silou a závaží na pružinu tahovou silou. Zavěšením závaží se změní délka pružiny.

Nákres:

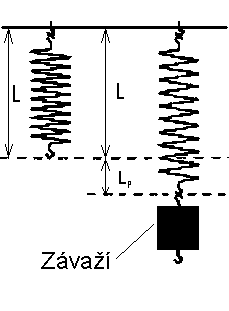L ... délka pružiny bez závaží L1 = L + Lp ... délka pružiny se závažím

 Téma: Hmotnost tělesa
 Úkol: Stanovte hmotnost pevného tělesa.

     Teoretická příprava: Hmotnost tělesa je fyzikální veličina a značí se m. Čím má těleso větší hmotnost, tím větší silou působí na podložku.

Přístroje pro měření hmotnosti - váhy

 Téma: Jednotky hmotnosti

Úkol:	1.Vyjádřete hmotnost tělesa v různých jednotkách
	2. Určete hmotnost drobných těles pomocí počítače a soupravy ISES.

     Teoretická příprava: Hmotnost tělesa můžeme vyjádřit v různých jednotkách. Nejčastěji se používají jednotky gram (g) a kilogram (kg).

Jednotky hmotnosti:

1kg ..... kilogram

1dag ..... dekagram

1cg ..... centigram

1g ..... gram

1mg ..... miligram

 Téma: Hmotnost kapaliny a sypké látky

Úkol:	1. Stanovte objem 25g sypké látky.
	2. Určete hmotnost 100ml kapaliny.

     Teoretická příprava: Při vážení sypké látky musíme mít na paměti, že každá změna na miskách se děje jen při zaaretovaných vahách. Při vážení kapaliny v kádince musíme od celkové hmotnosti odečíst hmotnost prázdné kádinky.

 Téma: Hustota
 Úkol: Určete hustotu pevné látky.

     Teoretická příprava: Hustota je fyzikální veličina, značí se  . Hustotu pevné látky nemůžeme změřit přímo, ale vypočítáme ji podle vztahu , kde m je hmotnost pevného tělesa a V jeho objem.

 Téma: Teplota
 Úkol: Sestrojte graf závislosti teploty vody na čase.

     Teoretická příprava: Teplota je fyzikální veličina, která se značí t. Měříme ji teploměrem a udáváme ve stupních Celsia (°C).

 Téma: Rychlost
 Úkol: Určete průměrnou rychlost tělesa

     Teoretická příprava: Průměrná rychlost tělesa je taková rychlost, kterou by se těleso muselo pohybovat rovnoměrným pohybem, aby určitou dráhu urazilo za stejný čas, jako při pohybu nerovnoměrném.
Platí: v_p = s_c / t_c , kde s_c je celková dráha a t_c je čas, za který těleso urazilo dráhu s_c.

 Téma: Úlohy o pohybu
 Úkol: Řešte složitější úlohy o pohybu

     Postup při řešení:

1. Přečteme si pozorně zadání úlohy
2. Zapíšeme zadané veličiny
3. Provedeme nákres
4. Promyslíme si řešení úlohy
5. Zapíšeme postup řešení
6. Provedeme číselné řešení úlohy
7. Je-li třeba, sestrojíme graf
8. Napíšeme odpověď

 Téma: Skládání sil
 Úkol: Pomocí měřicí soupravy ISES určete výslednici sil působících na těleso

     Teoretická příprava: Na těleso působí dvě síly:

1. stejného směru - výslednice má stejný směr jako obě síly a její velikost určíme součtem velikostí obou sil
2. opačného směru - výslednice má stejný směr jako větší z obou sil a její velikost určíme tak, že od velikosti větší síly odečteme velikost menší síly
3. různého směru - výslednici můžeme určit graficky

 

 Téma: Tření
 Úkol: Změřte velikost třecí síly při pohybu tělesa a experimentálně ověřte, na čem závisí.

     Teoretická příprava: Třecí síla působí proti pohybu tělesa v místě dotyku tělesa s podložkou. Značíme ji F_t. Jestliže se těleso působením tahové síly F pohybuje rovnoměrně přímočaře, je třecí síla rovna přímo tahové síle (výslednice obou sil je nulová). F = F_t.

 Téma: Páka

Úkol:	Ověřte podmínku pro rovnovážnou polohu páky
	1. působí-li síly na různých stranách od osy otáčení
	2. působí-li síly na stejné straně od osy otáčení

     Teoretická příprava: Páka je v rovnováze, jestliže platí: F₁.r₁ = F₂.r₂, kde F₁, F₂ jsou velikosti působících sil a r₁, r₂ jsou ramena působících sil.

 Téma: Kladka
 Úkol: Sestavte pevnou a volnou kladku a ověřte podmínku rovnováhy.

     Teoretická příprava: U pevné kladky nastane rovnováha pro F₁ = F₂, u volné kladky je síla, potřebná na zvednutí břemena poloviční než tíha břemena. Hmotnost volné kladky přičítáme k hmotnosti břemene.

 Téma: Archimédův zákon
 Úkol: Určete objem tělesa pomocí Archimédova zákona.

     Teoretická příprava: Archimédův zákon umožňuje určit vztlakovou sílu působící na těleso ponořené do kapaliny o dané hustotě.

 Téma: Opakování učiva

Úkol:	a) Seznámení s laboratorním řádem
	b) Výpočty příkladů z nižšího ročníku

     Teoretická příprava: Při řešení fyzikálních úloh většinou dodržujeme daný postup:

1. Přečteme si pozorně zadání úlohy
2. Zapíšeme zadané veličiny
3. Provedeme nákres
4. Promyslíme si řešení úlohy
5. Zapíšeme postup řešení
6. Provedeme číselné řešení úlohy
7. Je-li třeba, sestrojíme graf
8. Napíšeme odpověď

---

---

---

---

---

---

---

---

---

---

---

Úlohy pro kvarty

 Téma: Zpracování fyzikálních měření

Úkol:	1. Změřit hranu kvádru posuvným měřidlem
	2. Určit aritmetický průměr a odchylky měření

     Teoretická příprava: Měřit fyzikální veličinu znamená porovnávat její velikost s předem zvolenou jednotkou. Měření fyzikální veličiny je zatíženo chybami.

---

 Téma: Měření indexu lomu látky
 Úkol: Změřte index lomu skla

     Teoretická příprava: Index lomu udává kolikrát je rychlost světla v daném prostředí menší než ve vakuu. Měření budeme provádět na základě zákona lomu a pomocí totálního odrazu.

---

 Téma: Magnetické pole cívky

Úkol:	1. Prozkoumat vlastnosti magnetického pole cívky s proudem
	2. Sestrojit model elektromagnetu
	3.Pomocí počítače sledovat průběh indukovaného napětí a zakreslit výsledky pozorování

     Teoretická příprava: Kolem každého vodiče s proudem existuje magnetické pole. Vodič stočený do několika závitů se nazývá cívka. Elektromagnet je cívka s jádrem z měkké oceli.

---

 Téma: Transformátor

Úkol:	1. Ověřte činnost transformátoru v obvodu se stejnosměrným proudem
	2. Ověřte činnost transformátoru v obvodu se střídavým proudem
	3.Ověřte platnost transformačního poměru

     Teoretická příprava: Transformátor se skládá ze dvou cívek na společném jádře. Jedna cívka je připojena ke zdroji (primární), druhá cívka je v obvodu se spotřebičem (sekundární). Poměr napětí na sekundární a primární cívce se nazývá transformační poměr, značí se p a platí: p = U2/U1. Transformátor používáme k transformaci nahoru (U2 > U1) nebo k transformaci dolů (U2 < U1).

---

 Téma: Určení voltampérové charakteristiky spotřebiče
 Úkol: Sestrojte voltampérovou charakteristiku spotřebiče

     Teoretická příprava: Voltampérová charakteristika spotřebiče je graf závislosti proudu, který prochází spotřebičem na napětí na spotřebiči. Napětí na spotřebiči regulujeme potenciometrem. Při průchodu proudu spotřebičem vzniká teplo, spotřebič se zahřívá. Na průběh charakteristiky má vliv závislosti odporu na teplotě.

---

 Téma: Polovodičová dioda

Úkol:	1. Zapojení diody v propustném a závěrném směru
	2. Sestrojení V – A charakteristiky diody

     Teoretická příprava: Dioda je polovodičová součástka, která obsahuje jeden přechod P-N. Při zapojení diody v propustném směru je vodivá, při zapojení v závěrném směru obvodem neprochází měřitelný proud. Voltampérová charakteristika diody je závislost proudu na napětí na diodě.

---

 Téma: Měření ohniskové vzdálenosti čočky

Úkol:

Určete ohniskovou vzdálenost spojky přímou metodou.

    Teoretická příprava: Ze zobrazovací rovnice čočky 1/f = 1/a + 1/a´ platí pro ohniskovou vzdálenost f = (aa´)/(a + a´), kde a je vzdálenost předmětu od optického středu čočky, a´ je vzdálenost obrazu od optického středu čočky. Měřením a, a´ můžeme určit ohniskovou vzdálenost (přímá metoda). Vzdálenosti a, a´ se měří od optického středu čočky. Vzhledem k tloušťce každé reálné čočky je takové měření nepřesné. Proto se přímé měření ohniskové vzdálenosti obchází užitím různých metod. Nejčastěji se používá Besselova metoda.

---

 Téma: Měření ohniskové vzdálenosti čočky

Úkol:

Určete ohniskovou vzdálenost spojky Besselovou metodou

     Teoretická příprava: Vzhledem k tloušťce každé reálné čočky je měření ohniskové vzdálenosti přímou metodou (výpočtem ze zobrazovací rovnice) nepřesné. Proto se přímé měření ohniskové vzdálenosti obchází užitím různých metod. Nejčastěji se používá Besselova metoda. Besselova metoda je založena na poznatku, že pro jistou vzdálenost předmětu a stínítka existují dvě polohy čočky, při nichž vzniká ostrý skutečný obraz. V poloze I je čočka u předmětu – obraz je zvětšený, v poloze II je čočka u stínítka – obraz je zmenšený.

Úlohy pro kvinty

 Téma: Měření objemu pevného tělesa pravidelného tvaru

Úkol:	1. Seznámení s laboratorním řádem, BOZP a PO
	2. Určete objem dřevěného hranolu tvaru kvádru

     Teoretická příprava: Pro objem hranolu tvaru kvádru platí vztah V = a.b.c, kde a,b,c jsou délky hran hranolu.

     U této laboratorní práce si můžete také stáhnout návod na zpracování naměřených hodnot..

---

 Téma: Hustota tuhého tělesa
 Úkol: Určete hustotu pevné látky (v g.cm^-3), ze které je zhotoveno těleso.

     Teoretická příprava: Hustotu pevné látky nemůžeme rovnou změřit, ale musíme ji vypočítat podle definičního vztahu r = m/V, kde m určíme pomocí laboratorních vah, V vypočítáme z naměřených rozměrů.

---

 Téma: Počítání s vektorovými veličinami a výpočet průměrné rychlosti
 Úkol: Řešte příklady na počítání s vektory a průměrnou rychlostí

     Teoretická příprava: Vektorové veličiny jsou dány jednoznačně svou číselnou hodnotou, jednotkou a směrem. Při výpočtech musíme tento směr zohlednit. Průměrná rychlost je dána podílem celkové dráhy, kterou těleso urazí za čas t a tohoto času.

---

 Téma: Kinematika pohybu rovnoměrného a rovnoměrně zrychleného

Úkol:	1. Zjistěte, jaký druh pohybu koná kulička, kterou považujeme za hmotný bod, po vodorovné rovině.
	2. Určete velikost zrychlení kuličky při pohybu po nakloněné rovině.

     Teoretická příprava: Kuličku uvolníme z určitého bodu nakloněné roviny. Kulička urazí po nakloněné rovině dráhu s₁ za dobu t₁ pohybem rovnoměrně zrychleným. Pro tento pohyb platí:

     Po vodorovné rovině urazí kulička dráhu s₂ za dobu t₂. Průměrnou rychlost kuličky na vodorovné rovině vypočteme podle vztahu:

---

 Téma: Smykové tření
 Úkol: Změřte součinitele smykového tření a určete, na čem závisí.

     Teoretická příprava: Při pohybu tělesa po podložce vzniká na styčné ploše mezi tělesem a podložkou třecí síla F_t , pro jejíž velikost platí

---

 Téma: Pohyby těles v homogenním tíhovém poli (Vrhy)
 Úkol: Pomocí počítače modelujte pohyby tělesa v homogenním tíhovém poli

     Teoretická příprava: Pohyby v homogenním tíhovém poli jsou obecně pohyby složené z pohybu rovnoměrného přímočarého (konstantní rychlostí v₀) a z volného pádu. Výsledný pohyb nazýváme vrh.

---

 Téma: Přeměny energie

Úkol:	1. Teoretické řešení úloh na ráz těles.
	2. Praktické sledování přeměn různých forem mechanické energie.

     Teoretická příprava: Ráz těles je děj, při němž se tělesa o různé hmotnosti a různé rychlosti srazí a po srážce se opět pohybují. Rozlišujeme:
a) Dokonale nepružný ráz těles – při srážce se tělesa spojí a dál se pohybují jako jedno těleso. Platí zákon zachování hybnosti a neplatí zákon zachovaní kinetické energie
b) Dokonale pružný ráz těles – při srážce nedochází k žádné přeměně kinetické energie těles ani na deformaci ani na teplo. Po srážce se tělesa pohybují každé samostatně. Platí zákon zachování hybnosti i zákon zachování energie.

---

 Téma: Měření hustoty pevné látky
 Úkol:Změřte hustotu skla, z něhož jsou vyrobeny zkumavky.

     Teoretická příprava: Je-li skleněná zkumavka ponořena do vody ve větší nádobě a je zčásti naplněna vodou, tak při určitém objemu vody ve zkumavce horní okraj zkumavky poklesne do roviny hladiny vody ve větší nádobě. Z Archimédova zákona lze pak vypočítat hustotu použitého skla.

Úlohy pro sexty

 Téma: Veličiny molekulové fyziky
 Úkol: Řešte příklady

     Teoretická příprava: Mezi veličiny molekulové fyziky patří (mimo jiné) molární hmotnost, látkové množství, molární objem, relativní atomová a molekulová hmotnost ad.

---

 Téma: Přibližné určení průměru molekuly kyseliny olejové
 Úkol: Určete průměr molekuly kyseliny olejové

     Teoretická příprava: Když kapku kyseliny olejové kápneme na volný povrch vody, rozteče se a vytvoří na povrchu kapaliny tzv. monomolekulární vrstvu o výšce rovné průměru molekuly kyseliny olejové. Ze známého objemu kapky a obsahu plochy vrstvy se dá určit výška tenké vrstvy, a tím přibližně průměr uvažované molekuly. Protože z jedné kapky by se utvořila monomolekulární vrstva o obsahu až několika km², budeme používat roztok kyseliny olejové v benzínu. Benzín se na povrchu vypaří a velikost skvrny bude už podstatně menší.

---

 Téma: Měrná tepelná kapacita
 Úkol: Určete měrnou tepelnou kapacitu pevné látky užitím směšovacího kalorimetru

     Teoretická příprava: Probíhá-li mezi teplejším tělesem a studenější kapalinou v kalorimetru tepelná výměna, platí kalorimetrická rovnice. Pokud experimentálně určíme zbývající veličiny v kalorimetrické rovnici, můžeme vypočítat měrnou tepelnou kapacitu látky, ze které je těleso vložené do kalorimetru.

---

 Téma: Povrchové napětí kapalin
 Úkol: Určete povrchové napětí syntetického lihu kapkovou metodou

     Teoretická příprava: Při pomalém vytékání kapaliny ze svislé úzké trubice s rovným dolním okrajem se vytvoří na jejím konci kapka. Kapka se od trubice odtrhne, když povrchová síla působící na kapku podél obvodu v zúženém místě dosáhne rovnováhy s přibývající tíhovou silou kapky. K výpočtu povrchového napětí lihu použijeme srovnání s povrchovým napětím čisté vody při dané teplotě (srovnávací metoda).

---

 Téma: Mechanické kmitání

Úkol:	1. Modelujte pomocí počítače kmitavý pohyb
	2. Určete tuhost k pružiny pomocí pružinového oscilátoru

     Teoretická příprava: Mechanické kmitání je periodický pohyb tělesa kolem rovnovážné polohy. Pokud je časovým diagramem tohoto děje sinusoida (kosinusoida) mluvíme o harmonickém kmitání.

---

 Téma: Určení velikosti tíhového zrychlení matematickým kyvadlem
 Úkol: Určete tíhové zrychlení matematickým kyvadlem. Použijte vztah pro dobu kmitu T matematického kyvadla a odvoďte z něho výraz pro tíhové zrychlení g. Potřebné veličiny pro výpočet tíhového zrychlení zjistíte měřením.

     Teoretická příprava: Při malých amplitudách výchylky kyvadla mužeme pomocí vztahu pro periodu kmitání matematického kyvadla vypočítat tíhové zrychlení. Délka závěsu musí být co nejdelší.

---

 Téma: Měření indexu lomu látky
 Úkol: Určete index lomu skla na základě zákona lomu a totálního odrazu.

     Teoretická příprava: Pro chod paprsků skleněným půlválcem platí zákon lomu. Pokud změříme úhel dopadu a úhel lomu, můžeme vypočítat index lomu skla.

---

 Téma: Měření ohniskové vzdálenosti čočky
 Úkol: Určete ohniskovou vzdálenost spojky Besselovou metodou.

     Teoretická příprava: Besselova metoda je založena na poznatku, že pro jistou vzdálenost předmětu a stínítka existují dvě polohy čočky, při nichž vzniká ostrý skutečný obraz. V poloze I je čočka u předmětu - obraz je zvětšený, v poloze II je čočka u stínítka - obraz je zmenšený.

Úlohy pro septimy

 Téma: Laboratorní řád, elektrická měření – zásady
     Úkol:

     Teoretická příprava:

---

     Téma: Elektrické pole
     Úkol: Modelujte elektrické pole jednoho a dvou bodových nábojů pomocí počítače.

     Teoretická příprava: Elektrické pole vzniká v okolí elektricky nabitých těles. Dá se znázornit pomocí vektorů intenzity E (vektorový model), pomocí siločár (siločárový model) příp. pomocí ekvipotenciálních ploch (skalární pole - pomocí el. potenciálu).

 

---

 

     Téma: Kapacita kondenzátorů. Spojování kondenzátorů

Úkol:	1. Určete kapacitu samotných kondenzátorů
	2. Určete výslednou kapacitu různě spojených kondenzátorů

     Teoretická příprava: Kondenzátory jsou zařízení s velkou kapacitou. Dají se spojovat do soustav, jejichž výslednou kapacitu lze vypočítat.

     Připravený je i učební text kapacita a spojování kondenzátorů.

 

---

 

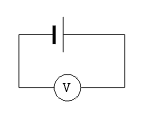
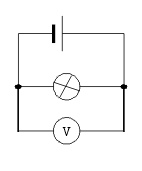
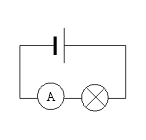
     Téma: Elektrické napětí. Proud.

Úkol:	1. Změřte napětí nezatíženého a zatíženého zdroje a určete odchylky
	2. Změřte proud procházející jednoduchým obvodem a vypočítejte odchylku

     Teoretická příprava: Podle schémat na obr. změříme napětí a proud pro různé rozsahy a určíme odchylky v jednotlivých měřeních.

 

---

 

     Téma: Zatěžovací charakteristika zdroje

Úkol:	1. Určete zatěžovací charakteristiku ploché baterky
	2. Určete zatěžovací charakteristiku stabilizovaného zdroje napětí

     Teoretická příprava: Zatěžovací charakteristika je závislost svorkového napětí zdroje na odebíraném proudu.
U_e . . . elektromotorické napětí zdroje
U . . . svorkové napětí zdroje
R_i . . . vnitřní odpor

 

 

---

 

     Téma: Elektrický odpor rezistoru

Úkol:	1. Změřte elektrický odpor rezistoru přímou metodou
	2. Změřte elektrický odpor rezistoru substituční metodou
	3. Změřte elektrický odpor rezistoru ohmmetrem

     Teoretická příprava: Konstrukce ampérmetru a voltmetru - základem je citlivý magnetoelektrický galvanometr, v němž se využívá silového působení magnetického pole na vodič s proudem. Při plné výchylce jím protéká proud I_G s napětím U_G. Odpor galvanometru je R_G = U_G / I_G

 

---

 

     Téma: Měření V - A charakteristiky spotřebiče
     Úkol: Určete V - A charakteristiku a) žárovky b) rezistoru c) termistoru.

     Teoretická příprava: V - A charakteristika je graf závislosti proudu procházejícího spotřebičem na napětí I = f(U)

1. Lineární charakteristika - vykazuje ji pasivní prvek - rezistor, jehož odpor je konstantní a platí pro něj Ohmův zákon. Grafem závislosti I na U je přímka.
2. Nelineární charakteristika - vykazují ji prvky, jejichž odpor není konstantní a závisí na procházejícím proudu. Pro tyto prvky neplatí Ohmův zákon. Grafem závislosti I na U je křivka (např. část paraboly)

 

 

---

 

     Téma: Polovodičová dioda
     Úkol: Sestrojte V-A charakteristiku polovodičové diody

     Teoretická příprava: Polovodičová dioda je elektrotechnická součástka s nelineární charakteristikou. Určujeme V-A charakteristiku při zapojení v propustném a závěrném směru.

 

---

 

     Téma: Stacionární magnetické pole

Úkol:	1. Modelujte magnetické pole jednoho a více vodičů s proudem pomocí počítače
	2. Výpočty velikosti magnetické indukce

     Teoretická příprava: Magnetická indukce charakterizuje silové působení magnetického pole na vodič s proudem a její velikost závisí jen na magnetickém poli.
Značka: B
Jednotka: T (tesla)

 

---

 

     Téma: Stacionární magnetické pole 2

Úkol:	1. Řešte teoretické úlohy
	2. Modelujte pohyb nabité částice v magnetickém poli

     Teoretická příprava: Částice s nábojem se při pohybu v magnetickém poli bude pohybovat po zakřivené trajektorii. Její tvar závisí na velikosti a znaménku náboje a velikosti magnetické indukce daného pole.

 

---

 

     Téma: Nestacionární magnetické pole

Úkol:	1. Řešte teoretické úlohy
	2. Sledujte průběh indukovaného napětí Ui

     Teoretická příprava: Při pohybu vodiče v magnetickém poli se na koncích vodiče indukuje napětí U_i , jehož velikost lze vyjádřit pomocí zákona elektromagnetické indukce.

 

---

 

     Téma: Usměrňovač střídavého proudu

Úkol:	1. Ověřit činnost polovodičového usměrňovače jednocestného
	2. Ověřit činnost polovodičového usměrňovače dvoucestného v tzv. Graetzově zapojení

     Teoretická příprava: V usměrňovači střídavého proudu se využívá základní vlastnosti polovodičové diody, kterou prochází proud jen v propustném směru, t. j. když je anoda kladná. V jednocestném usměrňovači prochází proud diodou jen v kladných půlperiodách střídavého napětí, které je pulsující (tepavé) a lze ho vyhladit pomocí kondenzátoru.o velké kapacitě. Při dvoucestném zapojení se používá čtyř diod, napětí pulsuje s dvojnásobnou frekvencí a lze jej snadno vyhladit. K dokonalému vyhlazení se používají filtry obsahující kondenzátory a odpory.

 

---

 

     Téma: Transformátor

Úkol:	1. Ověřte činnost transformátoru v obvodu se stejnosměrným proudem.
	2. Ověřte činnost transformátoru v obvodu se střídavým proudem.
	3. Ověřte platnost transformačního poměru.

     Teoretická příprava: Transformátor se skládá ze dvou cívek na společném jádře. Jedna cívka je připojena ke zdroji (primární), druhá cívka je v obvodu se spotřebičem (sekundární). Poměr napětí na sekundární a primární cívce se nazývá transformační poměr, značí se p a platí: p = U₂/U₁. Transformátor používáme k transformaci nahoru (U₂ > U₁) nebo k transformaci dolů (U₂ < U₁)